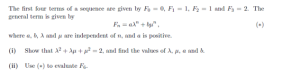Fortunately, just two weeks ago before Sarah Hart’s lecture I was guided to derive the formula for nth Fibonacci term by my Further Maths teacher, Imran Imam. The golden ratio simply dropped in our lap halfway through our solution. Is this just a coincidence with the number? Certainly not!
With some prior knowledge of this topic, I immediately grasped Sarah’s derivation: In a regular pentagon, the diagonal x is composed by one long line and one short line with length x-1 and 1 respectively. After rearranging, one of the solutions to the quadratic formed by equating ratios of the intersecting diagonals, is also equal to (1+sqrt(5))/2 the golden irrational number Φ. As the numbers in the ratio gets bigger, the ratio itself becomes converges, i.e. closer to the ‘standard ratio’, approximately 1.618.
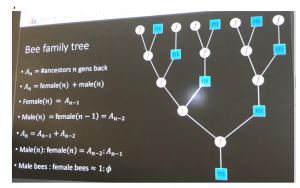
But we can see the golden ratio in nature! The bees follow an interesting sex-determination system called haplodiploïde: not all bees have to have two parents. Male bees hatch from unfertilised egg, i.e. they only have a mother. Female bees on the other hand, hatch from fertilised eggs and they have both parents. This implies that the population of male and female generation in a bee colony follows a Fibonacci sequence:1, 1, 2, 3, 5, 8…
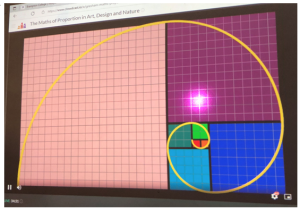
As an A2 Further Maths student, what I found the most interesting in this public lecture is the part on golden and logarithmic spirals as we have learnt from polar coordinates that the general polar form for a spiral is r=aΘ. The Fibonacci fact states that 1^2+1^1+2^2+3^2+…+Fn^2= FnFn+1. As the numbers expand, the distance from centre in golden spiral after turns is approximately square root of FnFn+1. Finally, you work out the distance ratio each quarter- turn which turns out to be Φ.
I felt inspired after attending this lecture and am grateful to Brampton College for arranging it. The lecture has taught me so much: not only about where the golden ratio comes from, but also its interesting supposedly biblical connotations and biological real life examples. I am applying to study Mathematics next year as are my peers who attended this lecture. I hope many years later, when I look back on this blog, by standing on a higher academic level, I will have more aspirations for my Mathematical studies, but still possess the enthusiasm I have for the subject today. Just like the nature of the Fibonacci sequence: the sum of the sequence from 0 to infinity tends to infinity, however the ratio between two consecutive Fibonacci numbers is convergent.
By Muyan Xu, student